2円の交点を内積で求める　finding the intersection of two circles using inner product

はじめに

　ある光波測距儀設置点ls_pからの複数の測点の結果があって，その測点のうち２点A, Bの3Dマップ上の座標値，（Xa, Ya）, (Xb, Yb)，が得られている場合，ls_pを求めることができる。なお，測量結果にはls_pから２点A, Bまでの水平距離HD，Ra, Rb，が含まれる。

　二つの円の交点を求める課題と同様で，すでに別のページで述べたように，二つの円の連立方程式を解く手法があるが，問題が出てきて，その対処に手間取った。

　次のWeb情報は極めて有効だが，ぼくからすると，簡潔すぎるので，ダサい補足説明を加えている。Microsoft Excelについても，多少，みかけだけだが，使いやすくした。
大矢建正のページ（数学，数楽 ＆ プログラム）（大矢さんは数学，数学教育，情報学が専門の元東海大学教授），の，

図形と方程式

２円の交点 [PDF]

Excel プログラム[xls]

概要

　図2は，当方のモデルである。2円の交点は，P₁とP₂である。この何れかに，光波測距儀の設置点 ls_pがある。計算式の作成上，慣例的に交点をP,Qとするより，理にかなっていると思っている。N（normal，大矢氏の記号はH）は，線分AB，線分P₁P₂の（垂直）交点にあたっている。

　計算結果は，次のようだ。
交点P₁の座標値：(Xp₁, Yp₁）
交点P₂の座標値：(Xp₂, Yp₂）

計算の考え方：

　円の幾何学から，ベクトルABとベクトルP₁P₂が直交することは自明である。その交点N上で，ベクトルABに直交するベクトルNP₁の単位ベクトルnを求めて，ベクトルNP₁，NP₂を得るという流れになる。 ベクトルの内積を利用した計算である。補足説明を加えてゆく。なお，この計算では慣例通り，NP₂はNP₁にマイナス符号をつける形で求めている。

ステップ1　線分AN長を求める

　図1の凧形でピタゴラスの定理を使って求める。

AN+BN=AB………式（1）

　但し，ABの値はピタゴラスの定理で自明

AN^2 – BN^2 = Ra^2 – Rb^2………式（2）

　但し，図1の凧形AP₁BP₂は直角三角形で構成されており，AN^2 = Ra^2 -NP₁^2，BN^2 = Rb^2 -NP₁^2が成り立つ。

AN – BN = (Ra^2 – Rb^2) / AB………式（3）

　但し，右辺の値は自明。式（2）から，AN^2 – BN^2 = (AN + BN)(AN – BN)ゆえに，AN – BN = (AN^2 – BN^2) / (AN + BN) = (Ra^2 – Rb^2) / AB。

AN =  (Ra^2 – Rb^2) / 2AB + AB/2………式（4）

　但し，右辺の値は自明。つまりはAN長を求めることができた。式（3）と式（1）から得られる。

　なお，Ra, ANが既知となるので，

P₁N = sqrt ( Ra^2 – AN^2)………式（5）

　次のベクトルの計算では，この線分ANと線分P₁N（NP₁）の長さを使う。

ステップ2　交点N上の単位ベクトルnを求めて交点P₁，P₂の座標を求める

ベクトルABに垂直な単位ベクトル n = ( (Yb – Ya)/AB, (Xa – Xb)/AB ) ………式（6）

　ここでは，内積を使って，あるベクトルに垂直なベクトルを求めている。ベクトルABとベクトルP₁P₂の交点であるN点で，ベクトルABのXY成分を入れ替えて、片方の符号を変えて、ベクトルABの線分長で割って、垂直な単位ベクトルが得られる。

ベクトル a = (a1, a2) に対して，ベクトルb = (b1, b2)が垂直の場合，内積はゼロになる。(a1, a2)・(b1, b2) = 0。式を整理すると，b1= ka2, b2=-ka1となる。このkがここの例では，1/ABにあたっている。

ベクトルNP₁ = +|P₁N| n  ………式（7）
ベクトルNP₂ = +|P₁N| n　………式（8）

交点の数

P₁N^2 = Ra^2 -AN^2 ………式（9）
が負の場合，共有点なし。が0の時は共有点が一つ（接点）。正の時は二つ。これは二次方程式の判別式にあたる。

エクセル計算

　大矢建正さんのエクセルファイルをほぼそのまま，利用させていただきます。当方の便宜上，タイトルなどは変更しました。図3は標準表示，図4は組み込み数式表示。H列には数式の参照セルを見る便宜上，G列の行番号を表示している。

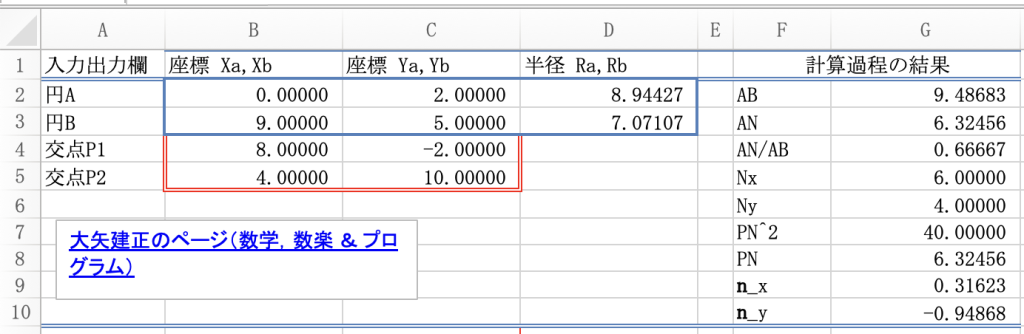
・G2では，ピタゴラスの定理で，線分AB長を求めている。

・G3では，式（4）で，ANを求めている。

・G4では，図2の線分AN/AB比を求めている。これはベクトルANのX座標比，Y座標比を求める準備である。

・G5，G6には，点Nの(X,Y)座標を求める計算式が入っている。この計算式内を下に列挙する。
　　Nx=B2+(B3-B2)*G4 ………式（10）
　　Ny=C2+(C3-C2)*G4 ………式（11）
　　G4は，線分AN/AB比ゆえに，円ABの中心の相対的な位置関係に関わらず，成立する。

・G7は，式（9）に対応する。実は式（9）は二次方程式の判別式に対応しているのである。式（9）を次に再掲する。式（9）：　P₁N^2 = Ra^2 -AN^2
ここでは，sqrt (P₁N^2)を設定することはできない。P₁N^2が負の場合もあるからである。2円の関係によっては，凧形AP₁BP₂は成立せず，点N，P₁N，ANは何も成立しない。図2のように凧形AP₁BP₂が成立して初めて，P₁P₂の交点2点が存在する。この場合，P₁N^2 > 0と表現できる。線分ABと線分P₁P₂の交点Nが円内に成立する。2円が接する場合というのは，線分AN = Raの場合で，P₁N^2 = 0と表現する。これ以外は，P₁N^2 < 0となる。
・図4左手の交点P₁P₂の4箇所の出力欄にはすべて，IF文が入っている。以下，列挙すると，
交点P₁のX座標：　IF (G7 < 0, ” “, G5+G9*G8) ………式（12）
交点P₁のY座標：　IF (G7 < 0, ” “, G6+G10*G8) ………式（13）
交点P₂のX座標：　IF (G7 < 0, ” “, G5- G9*G8) ………式（14）
交点P₂のY座標：　IF (G7 < 0, ” “, G6- G10*G8) ………式（15）
となる。共通部分は，IF (G7 < 0, ” “, 実行式)であるが，G7 < 0の場合，” “, つまり空白文字を出力し，G7 ≧ 0の場合は，式を実行せよ，となっているのである。実行式によって，交点P₁P₂のXY座標を得ることができる。

　残ったG列のG8には，PN = IF (G7 < 0, 0, SQRT(G7)，とあるが，判別式（G7）が負の場合，PN^2=PN=0としているので，自動的に2交点P₁P₂のXY座標値の出力欄は空白となる。G7 ≧ 0の場合は，sqrt(G7)だから，PN = P₁N = sqrt (Ra^2 -AN^2)となる。上記の式（12）〜（15）のG8にこの値が入る。

　最後のG9, G10は何を計算しているのか。式（6）を再掲する。
ベクトルABに垂直な単位ベクトル n = ( (Yb – Ya)/AB, (Xa – Xb)/AB ) ，について，n_xは (Yb – Ya)/AB，n_yは(Xa – Xb)/AB，に当たっている。
　交点P₁P₂のX座標については，式（12）と（14）が対応し，X座標値に関わっており，
G5+G9*G8 = Nx + n_x * P₁N となって，図2で見ると，点N + ベクトルNP₁
G5- G9*G8 = Nx − n_x * P₁N となって，図2で見ると，点N − ベクトルNP₁
を演算することになる。
　交点P₁P₂のY座標については，式（13）と（15）が対応し，X座標値に関わっており，
G6+G10*G8 = Ny + n_y * P₁N となって，図2で見ると，点N + ベクトルNP₁
G6- G10*G8 = Ny − n_y * P₁N となって，図2で見ると，点N − ベクトルNP₁
を演算することになる。

以上，Feb. 10, 2024記。

Web上での計算

円と円の交点座標計算　by s-project

以上