光波測量によるネットワークをdroneマップに投影する方法　how to match distance-measured points from different setting bases with a drone-measured map

1. 課題

　フィールドワークでの測量に問題が生じた。2020年測量のdrone３Dマップと，2018年の光波測距儀を使って得られたネットワークが対応しない。droneマップは光波測距儀で得られたgcpとの対応関係が取られている。そのgcpを使ってdroneマップをコントロールしているので問題はない。この場所には自衛隊のレーダーサイトがあって，コンパスが正常に作動していない危惧があり実際に西偏角度が想定されるものと異なっている。

　光波測距儀の設置点は14カ所で個々の設置点で幾つか測点があって，前視と後視で，位置関係を一応把握したのであるが，手抜きしてGPS計測値を光波測距儀の地球座標値として使用した。これが今抱える問題の元凶だ。そこで，2018年の測量時の測点の現場写真からdrone３Dマップと対応できる測点を利用して，ls_1〜_14の光波測距儀の設置点を求めたいと思う。

2. ls_2の設置点を求める

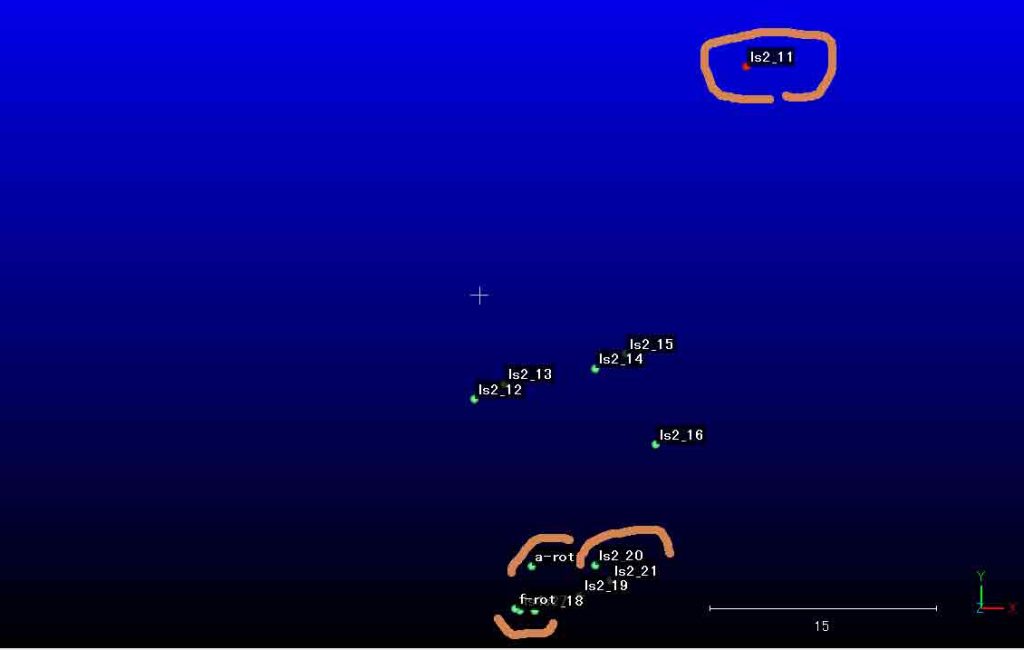
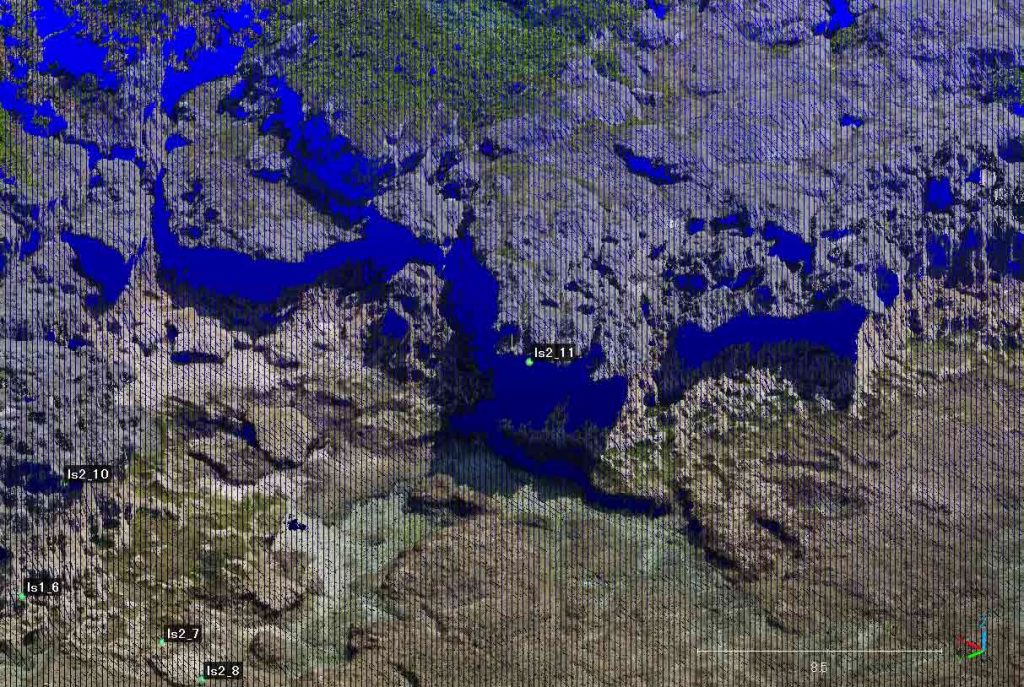
　ls_2の放射星形区で３Dマップ上での２カ所を現場写真から特定できた。その一つは，図１のls2_20であり，もう一つは図2のls2_11である。後者は光波ネットワークとも一致している。それを図3に示す。

　ls2_20の方は，図２に示すようにかなりズレている。図１の現場写真ではa-rotの下に見えるが，図2では3mほど内陸にずれ込んでいる。

　求めたいのは図１の，赤字で「かわぐち」としたls_2の設置点の３Dマップ上の座標値である。

3. ls_2の3Dマップ上の座標値を求める

3.1 計算法

　当初，3D空間での三角形平面を想定して計算すべきと考えた。しかしながら，熟考するとその必要性が無いことが明らかになった。光波測距儀の構造は台座を水平にして，光波測距儀が装着されている。コンパスで磁北をゼロ度として，台座上を時計回りに回転して，光波測距儀をターゲットに向けて，直線距離を求める。その測距儀の水平角と垂直角を記録する。これだけだ。今，問題なのは３Dマップでのls_2設置点を決定することであり，2D空間に過ぎない。

　連立方程式は簡単にできる。文字表現の簡略化したい。現在の設置点をO’点として，3Dマップに載せうる設置点をO点（Xo, Yo）とする。ls_2放射星形区の２点のうちの１点について，現在の位置をA’点として，3Dマップに載せうる設置点をA点（Xa, Ya）とする。他の１点については，現在の位置をB’点として，3Dマップに載せうる設置点をB点（Xb, Yb）とする。

　光波測量の結果から，次式が成り立つ。赤字表現しているのが未知数である。他の数値はすでに得られた計測値または3Dマップから読み取りできる。
|OA|=|OA’|=√((Xa-Xo)^2+(Ya-Yo)^2)　⋯⋯⋯⋯⋯式(1)
|OB|=|OB’|=√((Xb-Xo)^2+(Yb-Yo)^2)　⋯⋯⋯⋯⋯式(2)
　上記の計算式が成り立つ理由は次のようである。光波測量の結果に基づいて位置ベクトルを３Dマップにプロットするのであるが，ls_2の設置点が決まらないだけであって，その測定結果のうち，水平距離，垂直距離，さらには視準線の間の挟角は変わらない。

　式(1), (2)の連立方程式から，(Xo, Yo)の解が２個現れる。A点を中心として半径|OA|の円と，B点を中心として半径|OB|の円との交点は２点形成されるからである。3Dマップを見ている作者からするといずれが正解かは自明ではある。

　式(1)，(2) は何れも円の方程式である。両円は交わって，その二つの交点を通る直線が成立する。その観点で整理したいと思う。式(2)と(3)はそれぞれ，次のように整理できる。
(Xo– Xa)^2+(Yo– Ya)^2 = |OA|^2　⋯⋯⋯⋯⋯式(3)
(Xo– Xb)^2+(Yo– Yb)^2 = |OB|^2　⋯⋯⋯⋯⋯式(4)

　二つの交点を通る直線の式は，式(3) – 式(4)，で次のように，得ることができる。
2(Xa-Xb)Xo + 2(Ya-Yb)Yo +〔(|OA|^2 – |OB|^2) – (Xa^2 -Xb^2) – (Ya^2 – Yb^2)〕= 0⋯⋯式(5)

　両円の交点の計算は，式(3)と式(4)の何れかの円と式(5)の直線との交点を求めれば良い。ここでは，式(3)の円と式(5)の直線の交点を求めることにする。
　式(3)の，中心座標（Xa, Ya），半径 |OA|の円，と，式(5)の直線の交点をM, Nとして，交点を表現したいのであるが，かなり複雑になるので，式(5)を簡潔化して次に表現する。

e=2(Xa-Xb), f=2(Ya-Yb), g=〔(|OA|^2 – |OB|^2) – (Xa^2 -Xb^2) – (Ya^2 – Yb^2)〕として式(5)は次のようにする。
eXo + fYo + g = 0⋯⋯式(6)

以上，ここまで，Jan. 25, ’24記。

　さて，Microsoft Excelの計算式の書式で，交点MNの座標値を次に示す。

Xm=(e*D–f*sqrt((e^2+f^2)*|OA|^2-D^2))/(e^2+f^2)+Xa⋯⋯式(7)
Ym=(f*D+e*sqrt((e^2+f^2)*|OA|^2-D^2))/(e^2+f^2)+Ya⋯⋯式(8)

Xn=(e*D+f*sqrt((e^2+f^2)*|OA|^2-D^2))/(e^2+f^2)+Xa⋯⋯式(9)
Yn=(f*D–e*sqrt((e^2+f^2)*|OA|^2-D^2))/(e^2+f^2)+Ya⋯⋯式(10)

　なお，D=abs(e*Xa+f*Ya+g)⋯⋯式(11) とする。

　式(7)と式(9)，そして，式(8)と式(10)，の違いは第二項と第三項の間の符合に見える。

この計算プロセスを踏まえたMicrosoft Excelファイルは次節に用意する。

3.2 測量値などの準備

　ls_2放射星形区で，２カ所 ls2_11と_20の3Dマップ上の位置決めができている。ls2_11の座標値は変わらず，ls2_20だけを現場写真（図１）と対照して決定する必要がある。図4で特定している。光波測距儀による測量結果では，altitudeは1.171mだから，図4の右上に示した表では二行目が近い。まあ，これよりも海側下方であろうが，ほぼ対応しており，図4右上表の，Index 107222891を採用したい。
X: -96035.546875, Y: -625538.500000, Z: 1.243085

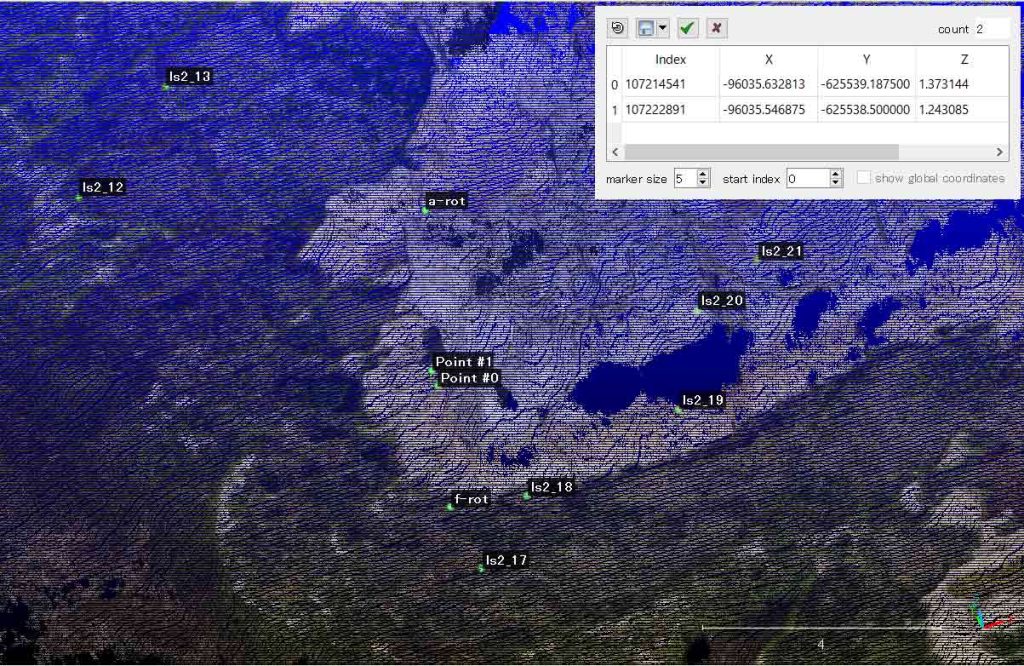
　以上から，式(3), (4)の既知数値は次のようになる。なお，注意すべきなのは世界測地系の (x, y)=(northing, easting)と3Dマップの(X,Y)=(easting, northing)は入れ替わっているということである。学校教育で使用するデカルト座標系に替わっている。繰り返すが，ls2_11の座標値は3Dマップと一致している。両円の半径は光波測距儀の読値HD horizontal distanceに対応している。

ls2_11を中心とする円関係：　(Xa, Ya)=(-96021.025, -625506.207), |OA|=42.830⋯⋯式(12)
ls2_20を中心とする円関係：　(Xb, Yb)=(-96035.547, -625538.500), |OB|=65.508⋯⋯式(13)

式(12), 式(13)は式ではないが，便宜上，式番号を与えた。「3.1 計算法」の計算プロセスをMicrosoft Excelに埋め込もうと思う。　

3.3 Microsoft Excel計算シート

　計算シートを作成し，実行した。しかしながら，ls2_20の3Dマップ上の認定を失敗したようで，求める結果を得ることはできなかった。そのプロセスは次の節にしめす。Microsoft Excelの計算シートでは，まずは次のテキストボックスを配置した。

————————————————

解　説

　３Dマップ上で特定された２地点から光波測距儀の設置点を求める手法をここに示す。

現在，設置点としてきたものをO’点として，3Dマップに適切に載せうる設置点をO点（Xo, Yo）とする。この例では，ls_2放射星形区の２点のうちの１点について，現在の位置をA’点として，3Dマップに載せうる設置点をA点（Xa, Ya）とする。他の１点については，現在の位置をB’点として，3Dマップに載せうる設置点をB点（Xb, Yb）とする。

　結局のところ，A点（Xa, Ya）を中心とする半径|OA|の円と，B点（Xb, Yb）を中心とする半径|OB|の円の交点を求める問題になる。連立方程式は次のようになる。

(Xo- Xa)^2+(Yo- Ya)^2 = |OA|^2　⋯⋯⋯⋯⋯式(1)
(Xo- Xb)^2+(Yo- Yb)^2 = |OB|^2　⋯⋯⋯⋯⋯式(2)

　交点MNの座標値を次に示す。

e=2(Xa-Xb), f=2(Ya-Yb), g=〔(|OA|^2 – |OB|^2) – (Xa^2 -Xb^2) – (Ya^2 – Yb^2)〕⋯⋯式(3) として，

Xm=(e*D–f*sqrt((e^2+f^2)*|OA|^2-D^2))/(e^2+f^2)+Xa⋯⋯式(4)
Ym=(f*D+e*sqrt((e^2+f^2)*|OA|^2-D^2))/(e^2+f^2)+Ya⋯⋯式(5)

Xn=(e*D+f*sqrt((e^2+f^2)*|OA|^2-D^2))/(e^2+f^2)+Xa⋯⋯式(6)
Yn=(f*D–e*sqrt((e^2+f^2)*|OA|^2-D^2))/(e^2+f^2)+Ya⋯⋯式(7)

なお，D=abs(e*Xa+f*Ya+g)⋯⋯式(8) とする。————————————————

　図５に，この計算部分を掲載する。

　図５のダウンロードファイルは用意しているが，ls_2放射星形区内の２点の選定について，試行錯誤の状態のため，成功の後のファイルを掲載したい。

3.4 計算結果の検証１

　図５の計算結果は，Ⅳ〜Ⅶに見えるが，位置関係から見ると，(Xm, Ym)を採用できる。内積計算でも評価できるが省略する。当方のMicrosoft Excelファイル Okinoerabujima川口木庭_2018Jun14 参考ファイルJan2024.xlsxの沖永良部島測量ls No.2では，ls_2の光波設置点はGeographicaで得られたGPS表示を採用しているが，その数値を，上記(Xm, Ym)に替えた。このスプレッドシートは，northing X, easting Yに設定しているので，図5の座標定義と逆になっているので注意が必要である。

　 ls_2の設置点を上記(Xm, Ym)に替えたのあるが，適切な結果が得られなかった。光波の視準線の磁北設定も変更する必要があった。もちろん，この視準角のゼロ位置を変更する必要性は当初から考えていたが，結局，3Dマップの真北設定でのXY座標値の土俵に入っているのだから，光波の測定値も磁北の偏角を考慮する部分は削除する必要があったのである。

　「図６　光波計測値の表に図５の計算結果を入力して磁気偏角をゼロに」を参照頂きたい。この計算過程を実施する前に，もともとのls_2の計算シート（沖永良部島測量 ls No. 2）をコピーして，この右隣に配置した。そして，最上行の「ls-site northing X」, 「ls-siti easting Y」カラムに，上記(Ym, Xm)を入力し，さらに，磁気偏角をゼロにするために，HRの角度を，補正済み真北からの角度，にそのまま，コピペした。その変更を赤字で示している。Loc. 11はls2_11に，Loc. 20はls2_20に該当している。もともとのls_2の計算シート（沖永良部島測量 ls No. 2）の値と比べると，ls2_11は，(x North, y East) = (0.19, 0.215)，ls2_20は，(x North, y East) = (0.46, 1.901)，となった。

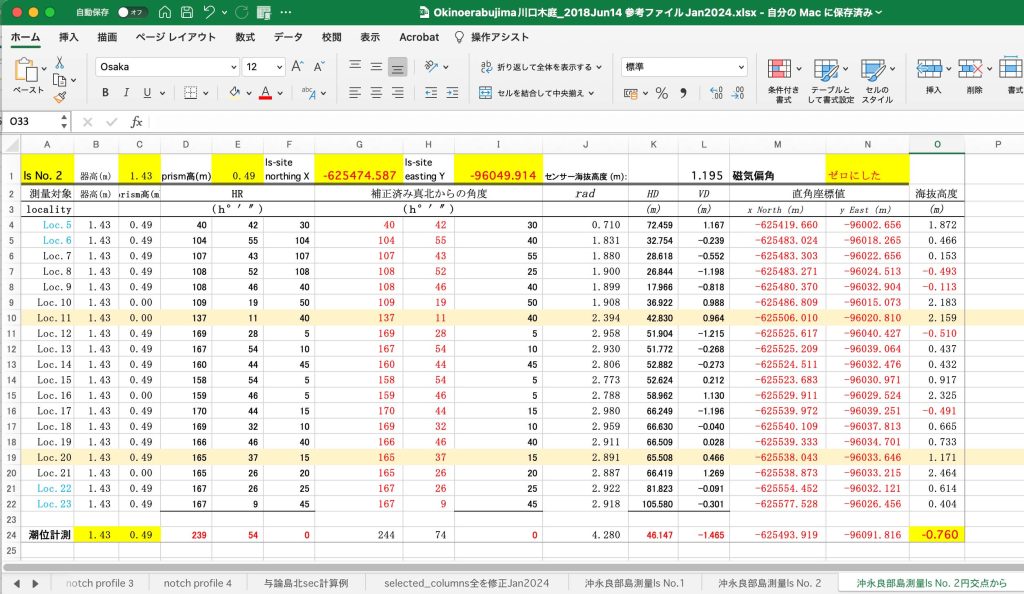
　この結果から，次の表に示したcsvファイルを作成し，CloudCompareに読み込んだ。

site_name	X easting	Y northing	altitude	Red	Green	Blue
ls2_5	-96002.656 	-625419.660 	1.872 	0	0	255
ls2_6	-96018.265 	-625483.024 	0.466 	0	0	255
ls2_7	-96022.656 	-625483.303 	0.153 	0	0	255
ls2_8	-96024.513 	-625483.271 	-0.493 	0	0	255
ls2_9	-96032.904 	-625480.370 	-0.113 	0	0	255
ls2_10	-96015.073 	-625486.809 	2.183 	0	0	255
ls2_11	-96020.810 	-625506.010 	2.159 	0	0	255
ls2_12	-96040.427 	-625525.617 	-0.510 	0	0	255
ls2_13	-96039.064 	-625525.209 	0.437 	0	0	255
ls2_14	-96032.476 	-625524.511 	0.432 	0	0	255
ls2_15	-96030.971 	-625523.683 	0.917 	0	0	255
ls2_16	-96029.524 	-625529.911 	2.325 	0	0	255
ls2_17	-96039.251 	-625539.972 	-0.491 	0	0	255
ls2_18	-96037.813 	-625540.109 	0.665 	0	0	255
ls2_19	-96034.701 	-625539.333 	0.733 	0	0	255
ls2_20	-96033.646 	-625538.043 	1.171 	0	0	255
ls2_21	-96033.215 	-625538.873 	2.464 	0	0	255
ls2_22	-96032.121 	-625554.452 	0.614 	0	0	255
ls2_23	-96026.456 	-625577.528 	0.404 	0	0	255

　図7を見ると，ls2_20などの位置はより左手（つまり海側）に移動しているが，例えばls2_18は，ls2_17付近に位置する必要がある。図8は新プロットだけを表示したものであるが，垂直関係に問題はないようであるが，図7のls2_19は本来，ls2_18が載っている緑藻の面の陸端に配置すべきものであり，光波測点が3Dマップとうまくフィットしていないことが見えるのである。

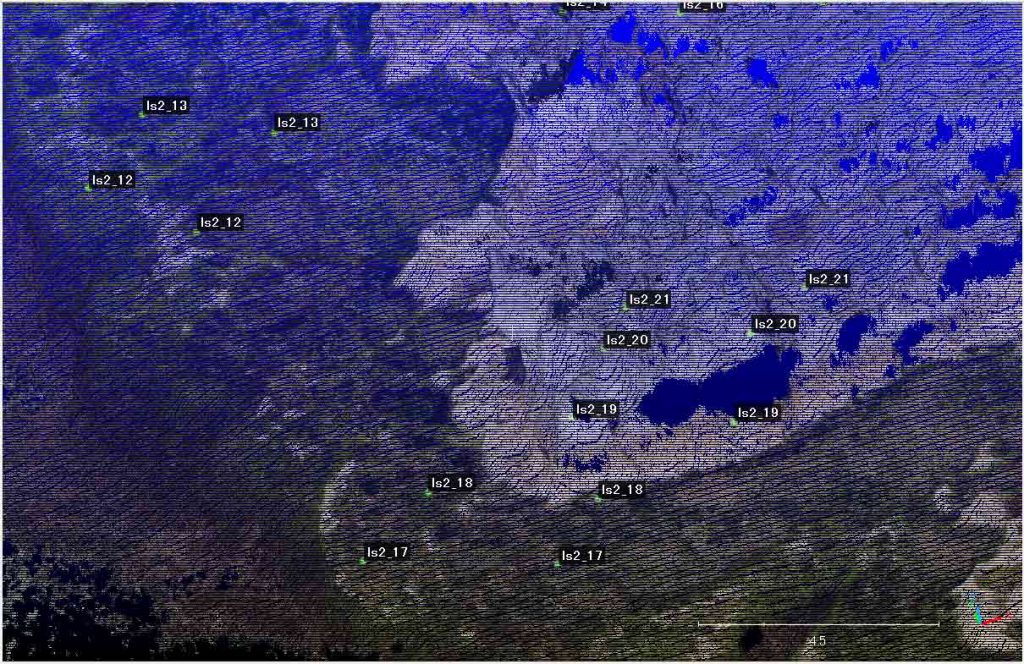
　結果からすると，ls2_20の3Dマップでの特定に誤りがあったようである。現場写真を見直して，ls2_19の方が特定しやすいように思われるので，これまでls2_20で実行したことを，ls2_19で試みることにした。

以上，14:36，Jan. 28, 2024記。

3.5 計算結果の検証２

　ls2_19の図10での想定位置位置を，図９の現場写真から決定した。図10の表の2の位置が適当と思われる。図10の鮮明度は低く，2階調にしている。このデータは次のようである。
X easting =-96036.617188, Y northing = -625539.000000, Z = 0.711838

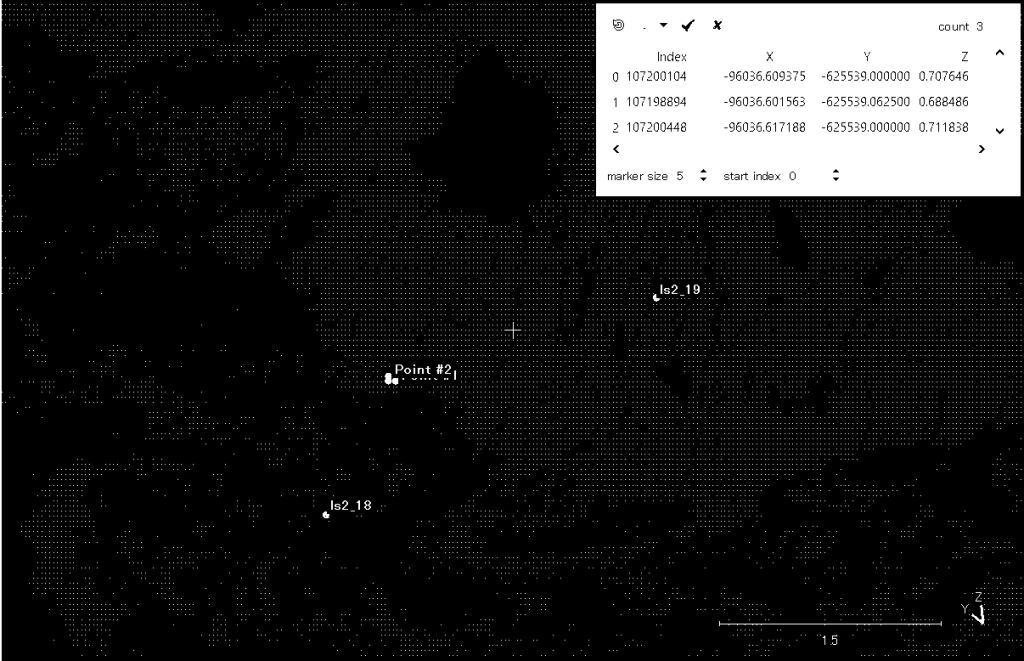
　ls2_11をCloudCompareで観察する限り，大きなズレはみにくいが，なにせ，drone撮影の影になっており，特定するのはかなり難しい。ls_19を採用してもうまく行かない場合は，ls2_11の代わりをみつける必要性がある。大変だなあ。

3.6 計算結果の検証3

　さて，これまで触らなかったls2_11に代わって，ls2_6（Z=0.466 m a.s.l.）の現場写真を観察して，3Dマップ上の座標値を求めた。図12右上のpicked points list表には２点が見えるが，下方の方を採用した。
　なお，図12のls2_6の海抜高度は高いように見えるが，Cloudを透過して表示されているからである。list picking作業で，水平位置が海側に移動することになる。

X easting = -96021.109375, Y northing = -625482.125000, Z = 0.445537である。

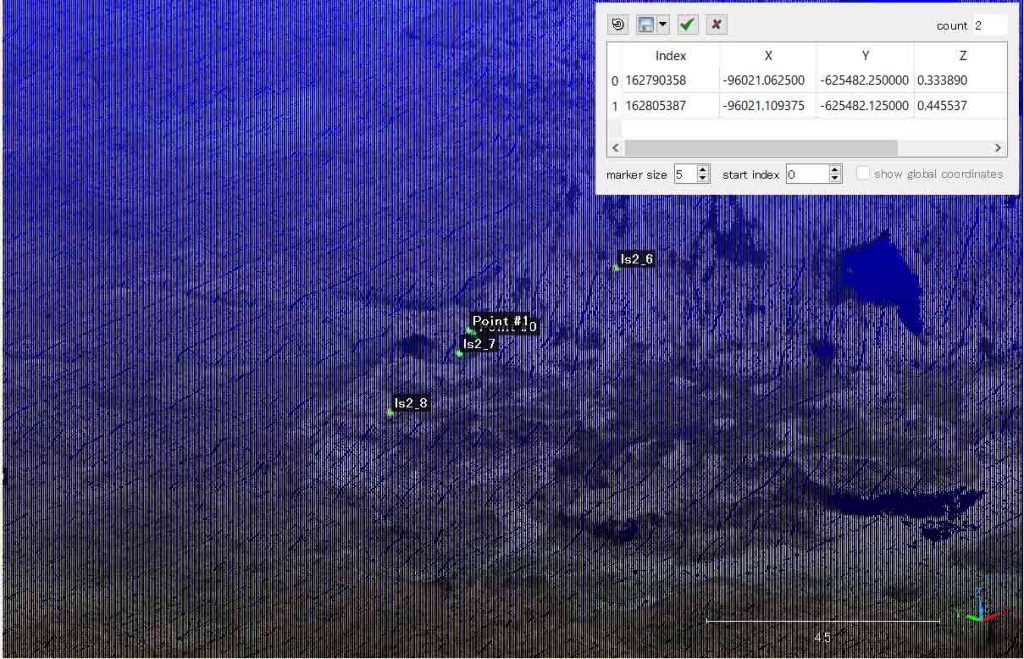
　このページは一昨日以来，触らなかった。ls2_6付近の表示の差を図13，14に示している。図2では北縁の測点はls2_11までしか見えていない。図13, 14の場所は図2よりも北方にある。図11のプリズム三脚の位置がls2_6にあたるが，図13では3Dマップ上のls2_6ポイントは，図11よりも更に内陸側に位置してる。図14を見ると，ls2_6は，いい按配に見える。それゆえ，両円の中心として，半径|OA|を作るA点をls2_11からls2_6に替えることで，大幅に改善されたことがわかる。

　このように，A点=ls2_6，B点=ls2_19,とすることで，図14のように，かなり改善を見た。では，ls2_19付近はどうなったのか。図7と比較すると，図15ではより改善され，光波の測点はより海側に移動した。

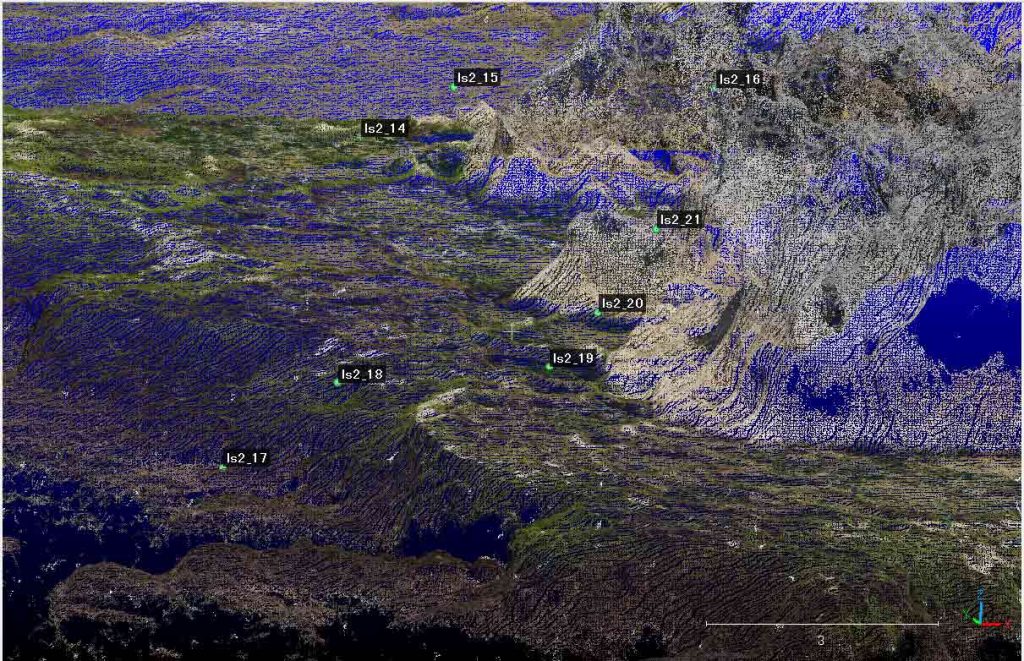
　A点をls2_11からls2_6に替えることで，ls2_6付近も，ls2_19付近も改善されたのである。ぼくの性格から，ls2_20とls2_6の組み合わせはどうかとやってみたが，劣化した。今のところ，ls2_6, ls2_19の組み合わせがいいようだ。

　図15で気になるのは海側にずれ込み過ぎていること，図16で気になるのは，ls2_6. _7, _8が左方にずれ込んでいることである。

　ls2_19付近の3Dマップと現場写真の対照はたぶん，これ以上の改善は難しい。ls2_6付近はどうか。これは悩んだ上での決定であったが，droneで撮影した空中写真の広域の方で見えるのではないか，と考えている。明日は，空中写真を判読して3Dマップと対照して，ls2_6の位置決めをしたいと思っている。

以上，23:18，Jan. 29, 2024記。

3.7 計算結果の検証4

　現場写真から，ls2_6をほぼ特定した。この海側（写真の上方）に波のスプラッシュが見えるが，これは図16のls2_7（Sw-spP）に対応するだろう。ls2_6は，Lw-spPだ。宇和美崎狭域3Dマップで，この場所を特定する必要がある。宇和美崎広域写真で特定したls2_6の位置だ。spratidal platformの陸端だ。

　図18には，宇和美崎狭域3Dマップ上で新たに特定したls2_6は，Point #1にあたる。

X= -96021.5703125，Y= -625484.5625, Z= 0.445600688457

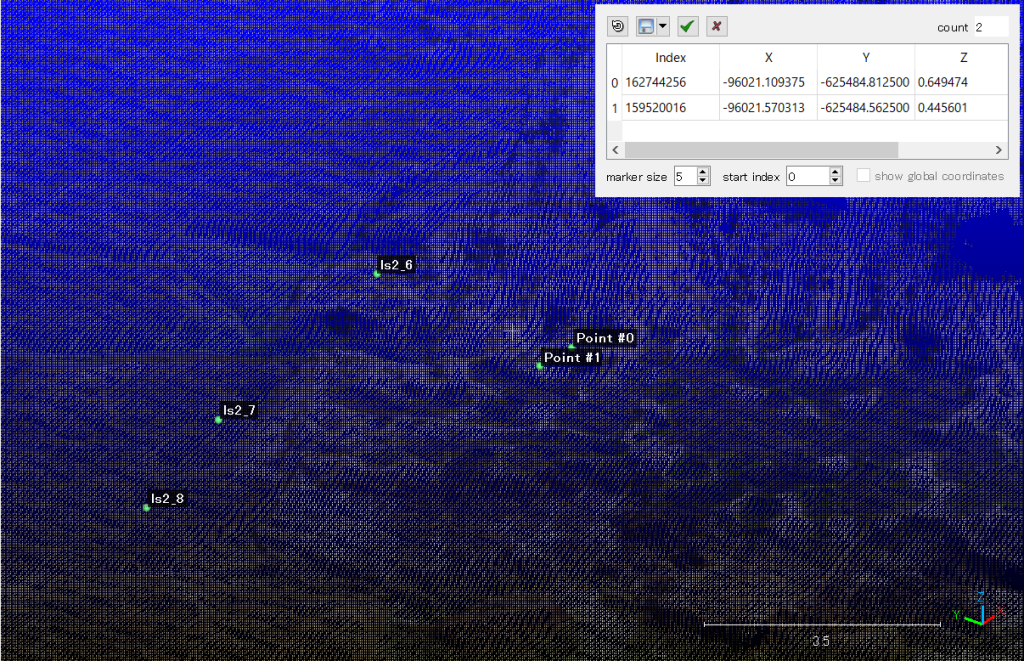
　やっと得たls2_6が新たなA点となる。B点（ls2_19）はすでに確定している。

　両円の交点をもとめ，それをls_2の設置点としてls2_5〜_23の（X, Y）を再計算してcsvファイル ls_2star_ls2_new6_19.csvを用意して，CloudCompareに読み込んだ。図19では，ls2_6付近のもので，右寄りのものが新たな結果で，フィールド写真とよく合っている。

　図20では，ls2_19付近のプロットで，過去で一番改善されたのであるが，いまだ，多少，海側にずれ込んでいる。

　これで，ls_2放射星域については終了しても良いが，ls2_19の位置決めを空中写真判読でも確認したいと思う。

以上，Jan. 30, 2024記。

3.8 計算結果の検証5

　ls2_19を写真（図9）を中心に，宇和美崎写真広域355, 356の実体視を加えて，検証した結果，あらたな位置を特定できた。図21には，新たにls2_19が特定されている（図中のPoint #0）。これまでの最新のプロットと対照すると，ls2_19などがより内陸側に移動できそうである。X= -96036.671875, Y= -625539.3125, Z= 0.754368662834となる。光波でのZ値は0.733m a.s.l.である。

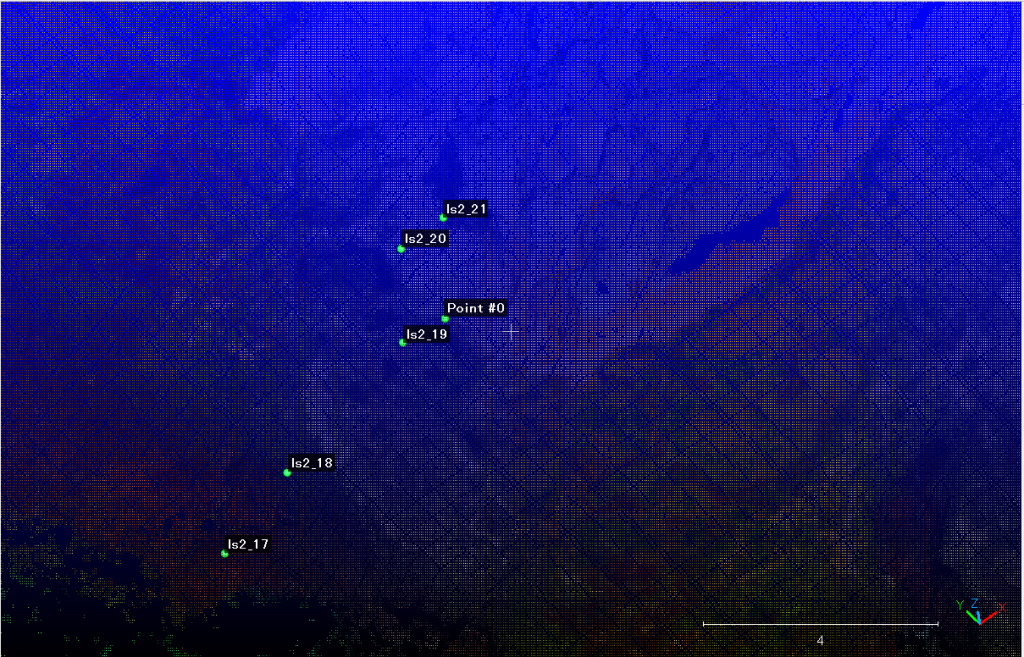
１　ls2_new6とともに，_new19が更新され，両円の交点を新たに得ることができる。
２　得られた交点をls_2光波設置点としてls2_5〜_23の（X, Y, Z）を求める。
３　Microsoft Excelシートからcsvファイルを作成。
４　CloudCompareで読み込んで宇和美崎狭域3Dマップ上にプロットする。

　この結果を次に。図22には，平行に配置されている同名のものの右下が新たなls2_19によるもので，本来，ls2_19であるべき場所のPoint #0には到達できていない。何故だろう。

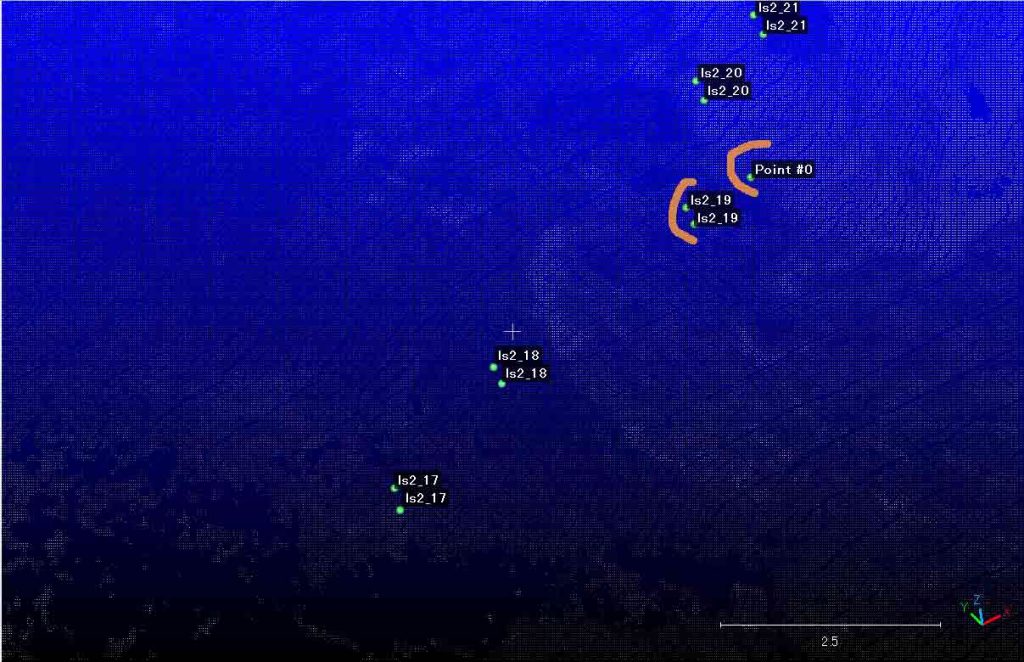
　 図23の結果は，図21の結果と極めて類似している。平行にズレている。さて？

以上，Jan. 31, 2024記。

4. 計算法を確認したい

4.1 問題の所在

　これまで述べてきたように，図22のPoint#0は，現場写真，空中写真を見つめて，3Dマップにls_19の位置と決定した場所に，CloudCompare上でPicking points list機能を使って，プロットした地点である。ベクトルOBの関連では，Oがls_2設置点で，BがこのPoint#0にあたる。両円の交点がOだから，|OB|=66.509mにあたる。光波測量の計算表に示しているように，|OB|は，HD horizontal distanceに当たっている。そういうように設定した訳だから，交点とls2_19の距離は，|OB|=66.509mの筈であり，宇和美崎狭域3Dマップ上のPoint#0と光波計算表のls2_19は一致する筈である。なのに，なぜ一致しないのだろうか。

　改めて，宇和美崎狭域3Dマップ上に描いた，ls_2光波設置点（図24のls_2setting）と，ls2_5〜23の分布を見たい。

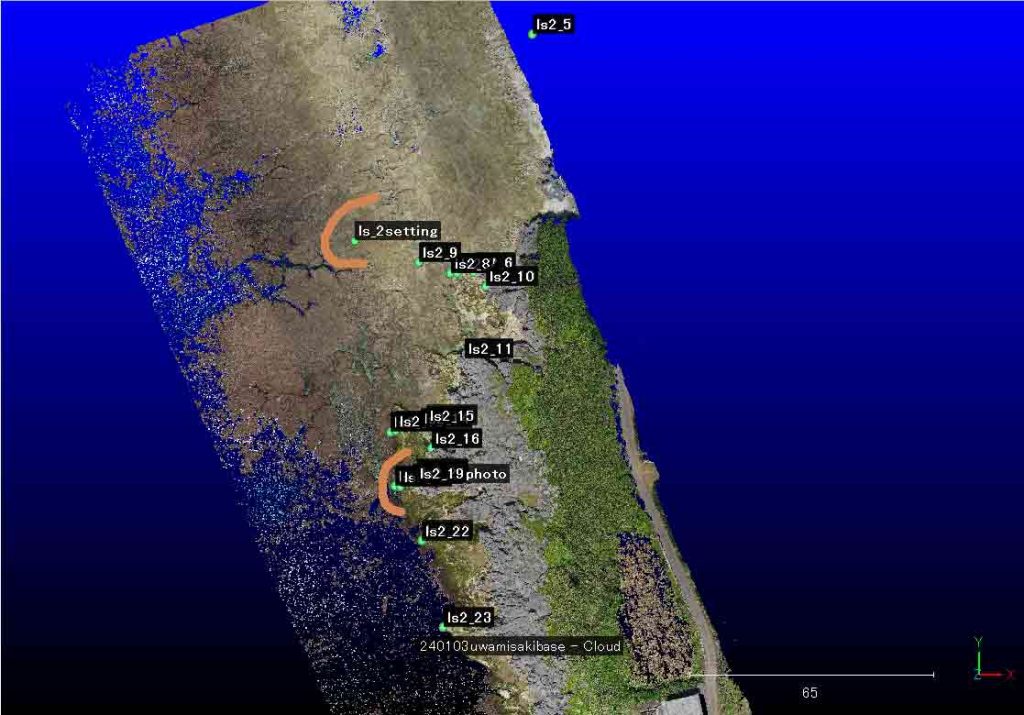
以上，Jan. 31, 2024記。

　両円の交点を求めるこれまでのプロセスを，図25のように図化した。何故に今採用している計算プロセスを経て得られたls2_19が現場写真から特定したPoint #1と一致しないのか，それを特定するためである。

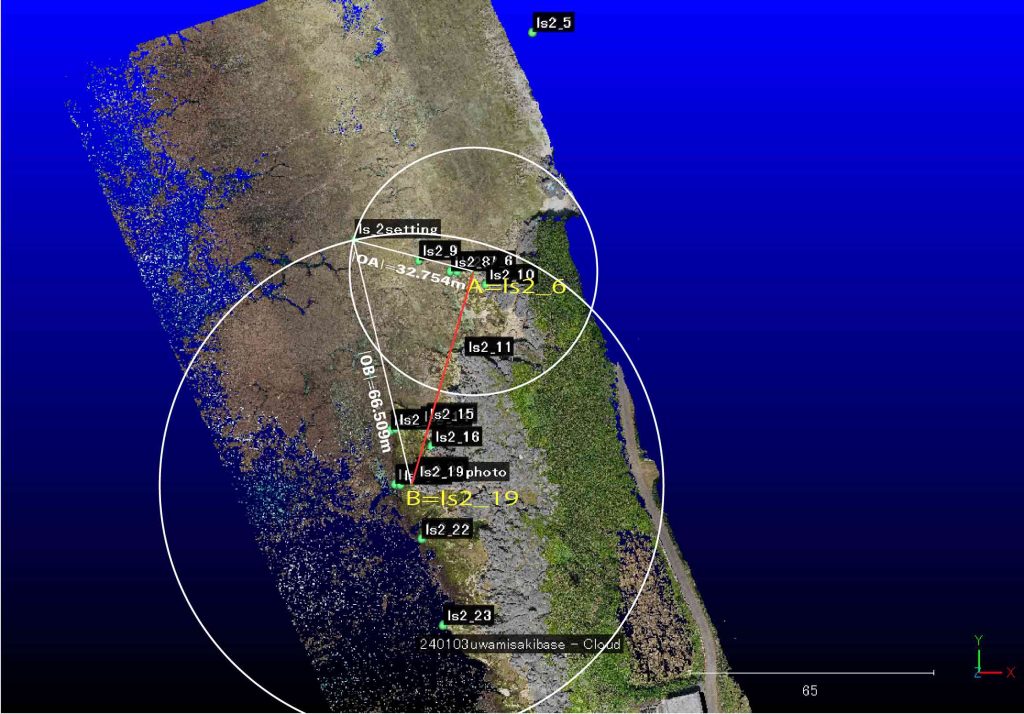
　これからのプロセスを確認すべく，流れを次に示す。

確認１　図25での両円の半径が正しく光波測距儀のHDと一致しているか。
　図25を評価する際に二つの面から調べる必要がある。点A, Bの座標値は，現場写真と空中写真から特定して3Dマップにpicking pointsの座標値にあたっている。これをここで，再掲したい。そしてMicrosoft Excelで計算して|OA|，|OB|が光波のHDに一致することを確認する。
　両円の交点を求めてそれをls_2設置点の座標値として，光波の計算プロセスで得られたls2_6, _19の座標値を使った場合，|OA|，|OB|が光波のHDに一致するか。まあ，一致しないだろう。しかし，一応，この結果を確認したいと思う。

確認２　１の検証結果は，光波の計算プロセスで歪みが生じたということになるだろう。では原因は何か。

確認３　まだやってないからわからないけど，まずは3Dマップが真北を捉えていない。gcpを使って適当に配置している。そして光波で得たネットワークを構成する放射星形区も真北がわからない。両方に原因がある。しかし，3Dマップに光波放射星形区を載せようということだから，3Dマップの擬似真北に光波の放射星形区も合わせないといけない。じゃあ，どうするか。
　図25のベクトルOAの時計回りの角度は，点ls_2settingの座標値を（Xo, Yo）として，現場写真と空中写真から特定された点ls2_19photoの座標値を（Xb, Yb）として，直角三角形の，角 [（Xb, Yo）（この頂点が直角）-（Xo, Yo）-（Xb, Yb）]を余弦定理から求めれば良い。その角度と光波測量時のHR（時計回りの回転角）を対照すれば，西偏用の角度補正のセルを変更すれば，ls_2設置点からの測点の(X, Y)座標値を得ることができるはずだ。

　楽しみだ。今日はタニハで疲れた。明日にした方がいいな。

以上，0:20，Feb. 2, 2024記。

　次にMicrosoft Excelで検証した結果を示す。
————————————————
1. OAとOBを半径とする円の中心と１交点
X Y Z
A相当：ls2_6photo -96021.570 -625484.563 0.446
B相当：ls2_19photo -96036.672 -625539.313 0.754
光波設置点：ls_2setting -96052.835 -625474.797 -0.235

2. |OA|と|OB|の距離と光波HDとの関係 計算結果 光波HD 評価
sqrt((Xa-Xo)^2+(Ya-Yo)^2) 32.754 32.754 当然，一致
sqrt((Xb-Xo)^2+(Yb-Yo)^2) 66.509 66.509 当然，一致
評価：　両円から交点を求めるプロセスに誤りはない。

3. 光波計算過程を得て得られたls2_new6, ls2_new19
X Y Z
ls2_new6 -96021.186 -625483.235 0.466
ls2_new19 -96037.622 -625539.543 0.733
光波設置点：ls_2setting -96052.835 -625474.797 -0.235

4. |OA’|と|OB’|の距離と光波HDとの関係 計算結果 光波HD 評価
sqrt((Xa-Xo)^2+(Ya-Yo)^2) 32.754 32.754 そうか，やっぱり一致
sqrt((Xb-Xo)^2+(Yb-Yo)^2) 66.509 66.509 そうか，やっぱり一致
————————————————

　両円の交点の計算過程でも，これを使った光波放射星形計算過程でも，|OA|, |OB|いずれも変質していないことがわかった。すぐ上の確認１〜確認３での思考プロセスに問題がないことがわかった。

4.2 3DマップのXY座標系に光波放射星形区のX’Y’座標系を合わせる

　用語が定まらないが，このタイトルで考えたいと思う。

　現場写真とdroneで撮影した空中写真を読み込んで，ls2_6とls2_19を中心とする円の交点を使ってきたのだが，点群の分解能と現場写真の質の点から，ls2_19の信頼性が高く，これを優先して計算過程を進めることになる。

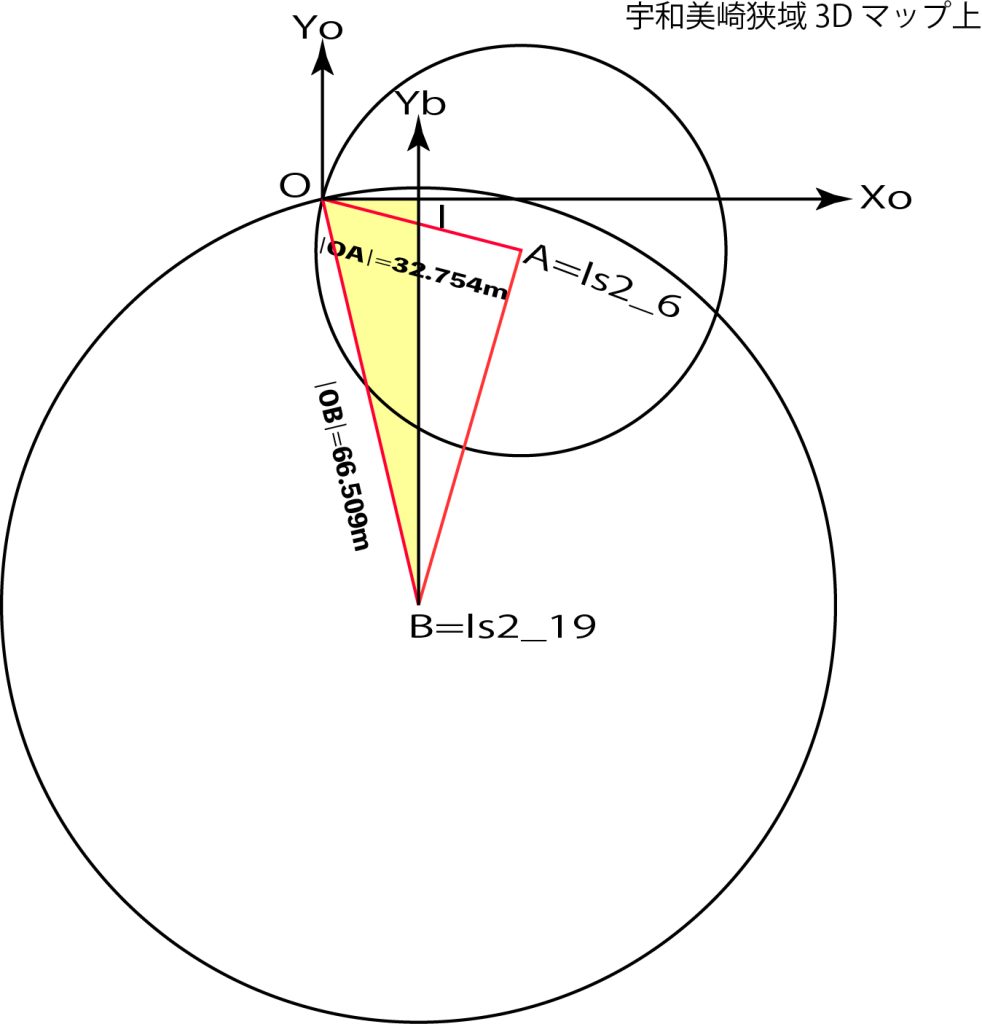
　図25の3Dマップの点群を非表示にして，Yo軸からls2_19軸までの時計回りの角度を求めたい。黄色で表示している△BOIに注目して，余弦定理で計算した。

————————————————
5. 余弦定理で直角三角形BOIの∠Oを求める
辺b=辺OI=|Xb-Xo| 16.163
辺i=辺BO=|OB| 66.509
辺o=辺IB=|Yo-Yb| 64.515
cosO: (b^2+i^2-o^2)/2*b*i 0.243
arccos(cosO) 1.325 radian
arccos(cosO)+p()/2 (Y軸からの時計回り) 2.896 ： 3Dマップ上での時計回りのOB角 radian
ls2_19のHRは166度46分40秒を度表示で 166.778
radianに変換 2.911 ：光波計算表でのHR radian
光波計算表でのHR補正値radian -0.015 radians
radiansからdegreesに変換 -0.841 degrees
degree + minute/60 + second/3600 -0°50′27.6″ ：この値を磁気偏角にして実行する。
————————————————
　上記の計算過程で，光波計算表で，実行した。
————————————————
6. 座標回転を考慮した光波計算過程で得られた地点Bと地点Aの（X, Y）座標の結果
現場写真3Dmap 光波座標回転後 差
OB: ls2_new19 Xb -96036.672 -96036.674 -0.002
OB: ls2_new19 Yb -625539.313 -625539.313 -0.000
結果評価： OB軸で座標回転したから当然一致する
OA: ls2_new6 Xa -96021.570 -96021.066 0.505
OA: ls2_new6 Ya -625484.563 -625482.769 1.793
結果評価： 次の項で述べる。
————————————————

この結果を使って，ls2_5〜_23の点情報のテキストファイルを作成して，CloudCompareに読み込んだ。その結果を次に示す。図27はls2_19付近，図28はls2_6付近である。解像度が低くて見にくいが，いずれも海岸地形の断面図作成用に設置した測点に完全に一致している。

　このウェブページ作成の目的を完璧に達成できているのである。

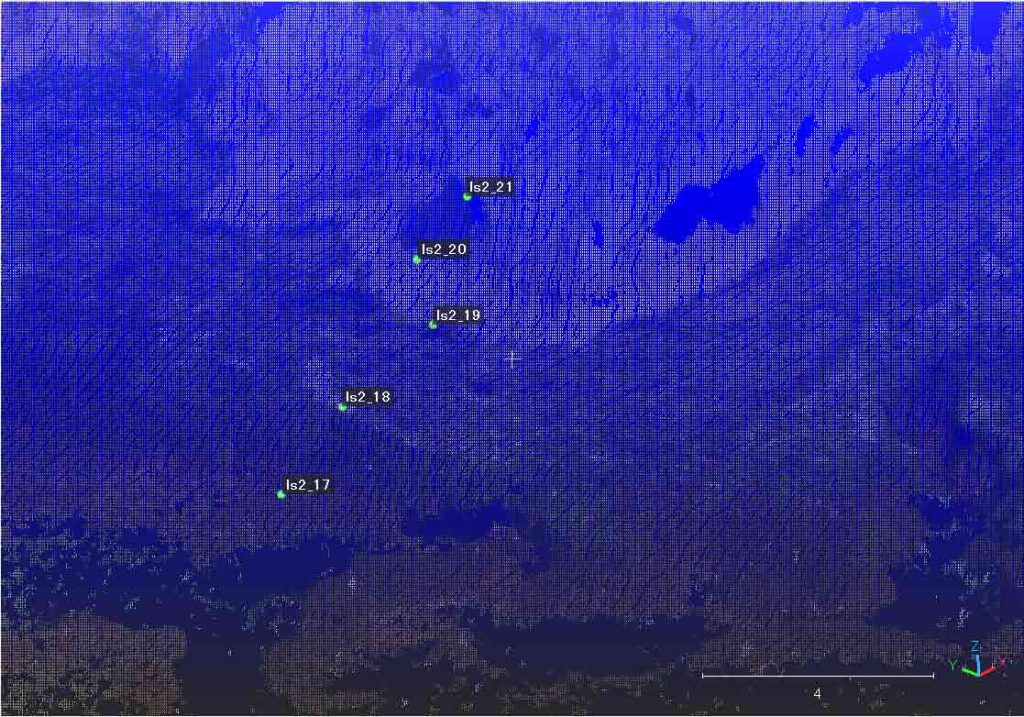
　ls2_19はベクトルOBを重視して，ls2_6の方も見事に達成できたのである。

　で，やっぱり，気になるのは，ls2_6つまり，OAの方である。計算してみた。
————————————————
7. OA軸についても座標回転の偏差を求めるかどうか
　一つの放射星形区で，現場写真から3Dマップとの関係での２地点を特定して，ベクトルOA, OB を中心とする半径HDa, HDbの円の交点を求めてそれを光波測距儀の設置点とするのであるが，地点A, Bを 特定して初めてこの作業が可能である。ここで示している例２．ではOBから光波測量結果をまとめた のであるが， OAについてもこの作業をする意味はない。地点A,Bでは，Aの方が信頼性が高く，Aの結果から得た偏角を採用して光波測量値を処理するしかない。
　光波のOA, OBの視軸がなす角度は，HRb’ – HRa’から得ることができる。radianでは，2.896-1.817=1.079である。一応，ここでのHRb – HRa を求めてみよう。直角三角形 BOAの∠BOAを次に求めてみる。

地点A, Bの座標値を再掲する。
X Y
A相当：ls2_6photo -96021.570 -625484.563
B相当：ls2_19photo -96036.672 -625539.313

辺b=辺OA 32.754
辺a=|OB| 66.509
辺o=辺AB 56.795
十進角（º）
cosO: (b^2+a^2-o^2)/2*b*a 0.521
arccos(cosO) = (HRb-Hra) 1.023 58.590
挟角の差　(HRb-Hra) – (HRb’ -Hra’) radian -0.056 -3.233
なお，(HRb’ – Hra’)は， 1.079 61.822
OA軸のY軸からの時計回り角度 radian 1.873 107.339
ls2_6の時計回り角度 radian 1.817 104.106

光波計算表でのHR補正値radian 0.056 3.233
：OAを採用すると補正角
————————————————

　以上で，一応納得の行く結果となった。
以上，Feb. 3, 2024記。

5. ls_2放射星形区の結果を使って次はls_1区

　これまでの努力で，ls_2は完成した。これに隣接する，ls_1とls_3にアタックすることになるが，まずは_1を。ただし，今のところ作成できた3Dマップは宇和美崎狭域のもので，ls_1の範囲の全域がカバーされていない。広域の3Dマップは未完成だ。
　放射星形区の間では，必ずしも２点での前視後視を実施していないが，ls_1とls_2の間では実行しており，Locs. 5, 6がそれに該当する。3Dマップとの対応関係はls_2で成功したので，ls_1の光波設置点は，ls2_5, 6の(X,Y)値を使って実行できるはずである。

5.1 新たなls_1の座標値を求める

　前掲の「3.ls_2の3Dマップ上の座標値を求める」，のプロセスをまずは実行することになる。(X, Y)値はls_2で最終的に得られたLocs 5, 6の値をls_1のそれとして代用することになる。HDについては，ls_1からのHDを使用する 。
easting 　 northing HD (ls_1)
ls2_5（ls1_5) 点A -96006.388 -625419.183，72.459 （過ってls_2のもの），72.465 （正しくls_1のそれ）
ls2_6 (ls1_6) 点B -96021.066 -625482.769 ，32.754（過ってls_2のもの），33.157（正しくls_1のそれ）

「3Dマップ上の2点から光波測距儀設置点を求める.xlsx」には問題があった。新しく2円の交点を内積で求める（２円交点EnToEn_revised.xlsx）を作成して両円の交点は２点得られた。Google Earthにプロットした旧来のls1_5, _6，GPSのls_1の配置からみて，Xm=-96053.17945, Ym= -625474.51596をls_1設置点と決定することができた。

5.2 新たなls_1の光軸回転角を求める

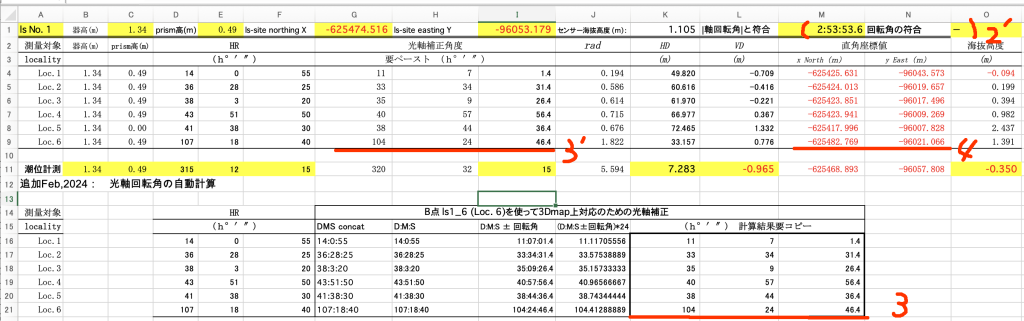
　「Okinoerabujima川口木庭_2018Jun14参考ファイルJan2024.xlsx」に，上記で得られた新たなls_1設置点の座標値を，入力した。すでにこのページで議論してきたように，さらに，光波測量の放射星形区の測量結果の座標回転が必要になる。「4.4 3DマップのXY座標系に光波放射星形区のX’Y’座標系を合わせる」，で述べた作業を実施する。△BOAを点O（新ls_1）の回りに回転するが，OA軸，OB軸の何れを使用するかで多少異なるが，現場写真を見ると，未完の宇和美崎広域３Dマップがたとえ後に完成しても，点A (ls1_5)を3Dマップにプロットするのは難しい。そこで，OB軸の回転角度を求めることにした。結果として，△の頂点と辺の名称はほぼそのまま使用できる。使用Microsoft Excelファイルは，「3Dmap上で光波星形区をフィット両円交点と座標回転.xlsx」（前掲のファイル名をより一般化してみた）にあたる。その計算シートを図29に示す。

　第29行（赤線の１）にはには余弦定理を使って求めた十進度104.413が見える。第31行（赤線１’）では，それをDMS表示に変換している。そして，その値をls_1星形区のLoc. 6 (ls1_6) のHR(DMS)で差し引いた結果が，赤線２に示す-02:53:53.6である。DMSの引き算の結果は➕️である必要があり，それを，第21〜27行右手に見えるテキスト枠に示している。第34行はその演算行にあたる。

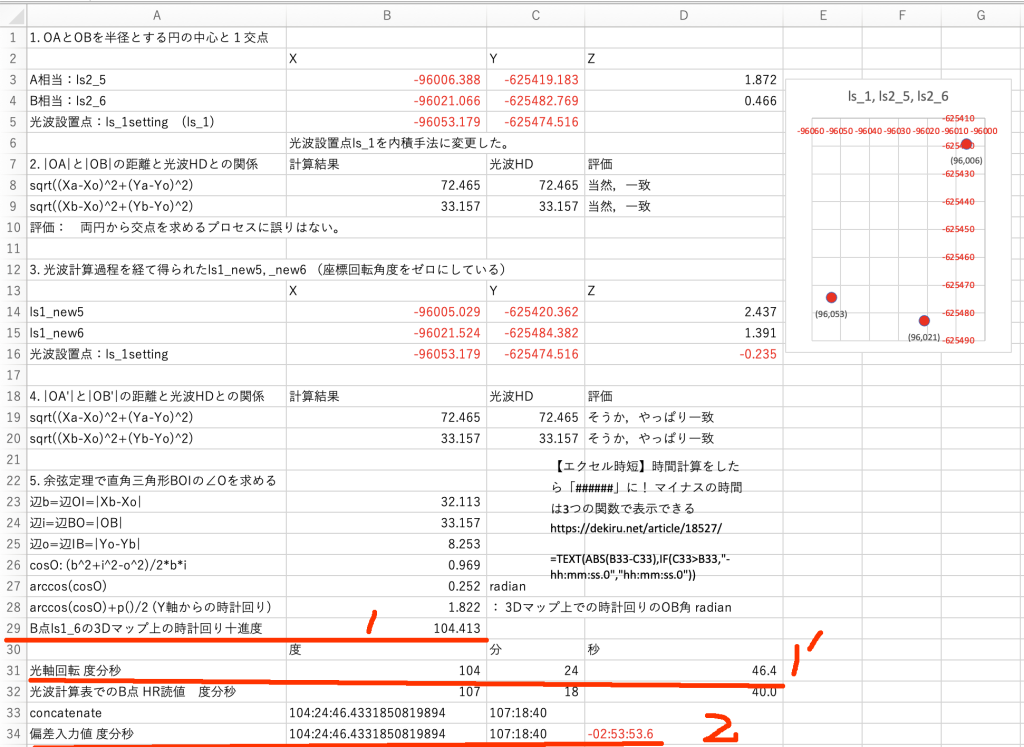
　この「偏差入力値」を使って，ls_1星形区のLocs. 1〜6の再計算を実施する。

　この後の計算の流れは，Microsoft Excelで度分秒表示角の差を求める ，「3. 光波測量結果に」に示している。その図５を，ここでは図30として再掲した。

　これまで述べてきた手法で，ls_3以降の星形区の光波結果を再計算したいと思っている。

　次の図31はCloudCompareで表示したところである。ls1_1〜_6とls2_5〜_13である。

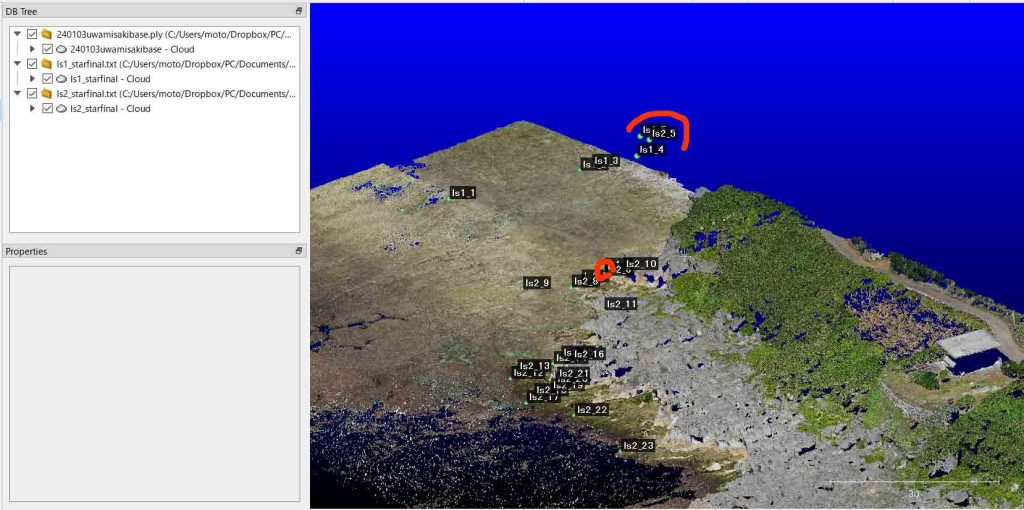
以上，Feb. 19, 2024記。